Discorsi e dimostrazioni
matematiche, intorno à due nuove scienze Leida 1638
Arutlused
ja matemaatilised tõestused kahest uuest teadusest
Leiden 1638
In un regolo, o vogliàn dir corrente,
di legno, lungo circa 12 braccia, e largo per un verso mezo bracio e
per l'altro 3 dita, si era in questa minor larghezza incavato un
canaletto, poco più largo d'un dito; tiratolo drittissimo, e, per
averlo ben pulito e liscio, incollatovi dentro una carta pecora
zannata e lustrata al possibile, si faceva in esso scendere una palla
di bronzo durissimo, ben rotondata e pulita; costituito che si era il
detto regolo pendente, elevando sopra il piano orizontale una delle
sue estremità un braccio o due ad arbitrio, si lasciava (come dico)
scendere per il detto canale la palla, notando, nel modo che appresso
dirò, il tempo che consumava nello scorrerlo tutto, replicando il
medesimo atto molte volte per assicurarsi bene della quantità del
tempo, nel quale non si trovava mai differenza né anco della decima
parte d'una battuta di polso. Fatta e stabilita precisamente tale
operazione, facemmo scender la medesima palla solamente per la quarta
parte della lunghezza di esso canale; e misurato il tempo della sua
scesa, si trovava sempre puntualissimamente esser la metà
dell'altro: e facendo poi l'esperienze di altre parti, esaminando ora
il tempo di tutta la lunghezza col tempo della metà, o con quello
delli duo terzi o de i 3/4, o in conclusione con qualunque altra
divisione, per esperienze ben cento volte replicate sempre
s'incontrava, gli spazii passati esser tra di loro come i quadrati e
i tempi, e questo in tutte le inclinazioni del piano, cioè del
canale nel quale si faceva scender la palla; dove osservammo ancora,
i tempi delle scese per diverse inclinazioni mantener esquisitamente
tra di loro quella proporzione che più a basso troveremo essergli
assegnata e dimostrata dall'Autore. Quanto poi alla misura del tempo,
si teneva una gran secchia piena d'acqua, attaccata in alto, la quale
per un sottil cannellino, saldatogli nel fondo, versava un sottil
filo d'acqua, che s'andava ricevendo con un piccol bicchiero per
tutto 'l tempo che la palla scendeva nel canale e nelle sue parti: le
particelle poi dell'acqua, in tal guisa raccolte, s'andavano di volta
in volta con esattissima bilancia pesando, dandoci le differenze e
proporzioni de i pesi loro le differenze e proporzioni de i tempi; e
questo con tal giustezza, che, come ho detto, tali operazioni, molte
e molte volte replicate, già mai non differivano d'un notabil
momento.
Võeti 12 küünra pikkune, poole
küünra laiune ja kolme sõrme paksune puidust pruss. Selle servale
lõigati veidi vähem kui sõrmelaiune renn. Kui see soon oli tehtud
vaga sirgeks, ühtlaseks ja siledaks, kaetud pärgamendiga, mis oli
samuti võimalikult sile ja poleeritud, veeretasime seda mööda
kõva, siledat ja väga ümarat pronksist kuuli.
Asetanud prussi kaldasendisse, tõstes
ühe otsa küünra või kahe võrra teisest kõrgemale, veeretasime
kuuli nagu ma just seletasin, mööda renni, määrates allaveeremise
aja viisil, mida ma hiljem seletan. Kordasime katset mitu korda, et
mõõta aega täpsusega, mille korral kahe vaatluse erinevus ei
ületaks kunagi kümnendikku pulsilöögi ajast.
Pärast sellise toimingu läbiviimist
ja olles veendunud selle usaldusväärsuses, lasime kuulil nüüd
veereda ainult veerandi renni pikkusest. Olles mõõtnud allaveeremise
aja, leidsime, et see on täpselt pool eelmisest. Järgmisena
proovisime teisi vahemaid, võrreldes kogu pikkuse läbimise aega
poole, kahe kolmandiku, kolme neljandiku või isegi suvalise
vahemikuga. Neis katsetes, mida korrati vähemalt sada korda,
leidsime alati, et läbitud vahemaad olid samas suhtes nagu veeremise
aegade ruudud ja see kehtis kõigi kaldpinna (st renni mida mööda
kuulid veeresid) kallete korral. Me täheldasime ka seda, et
erinevate kallete korral on veeremise ajad omavahel täpselt selles
suhtes, mida Autor on ennustanud ja demonstreerinud, nagu me näeme
hiljem.
Aja mõõtmiseks kasutasime me suurt,
kõrgele paigutatud veeanumat. Anuma põhja külge oli joodetud
väikese läbimõõduga toru, mis andis peene veejoa. Vee kogusime me
väiksesse klaasi iga allaveeremise ajal, olgu kogu renni pikkuses
või selle mingi osa ulatuses. Kogutud vesi kaaluti iga veeremise
järel väga täpsetel kaaludel. Nende kaalude erinevused ja suhted
andsid meile aegade erinevused ja suhted nii suure täpsusega, et
kuigi katseid korrati palju-palju kordi, polnud tulemustes tühistki
lahknevust.
Olgu, Galilei ei visanud tornist kuule alla, aga äkki keegi teine ikkagi viskas. Miks mitte, kindlasti keegi kuskil seda tegi.
Haamer ja sulg.
Brian Cox näitab suurt.
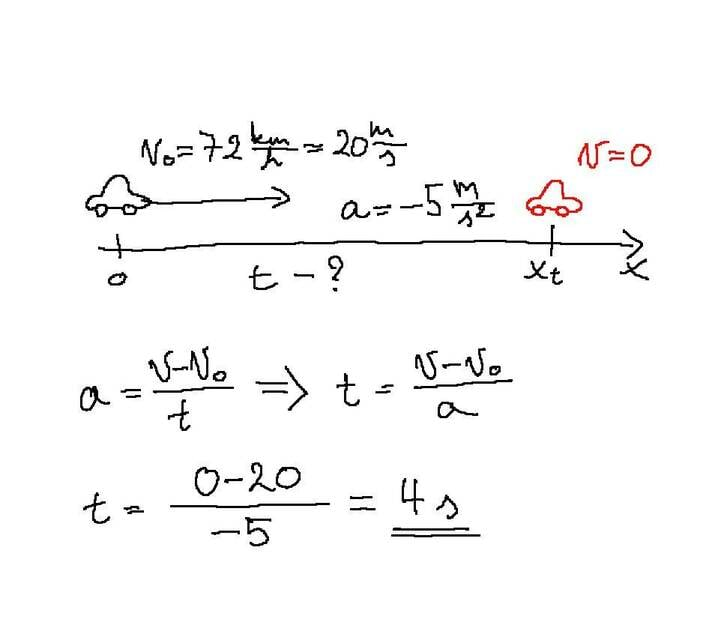
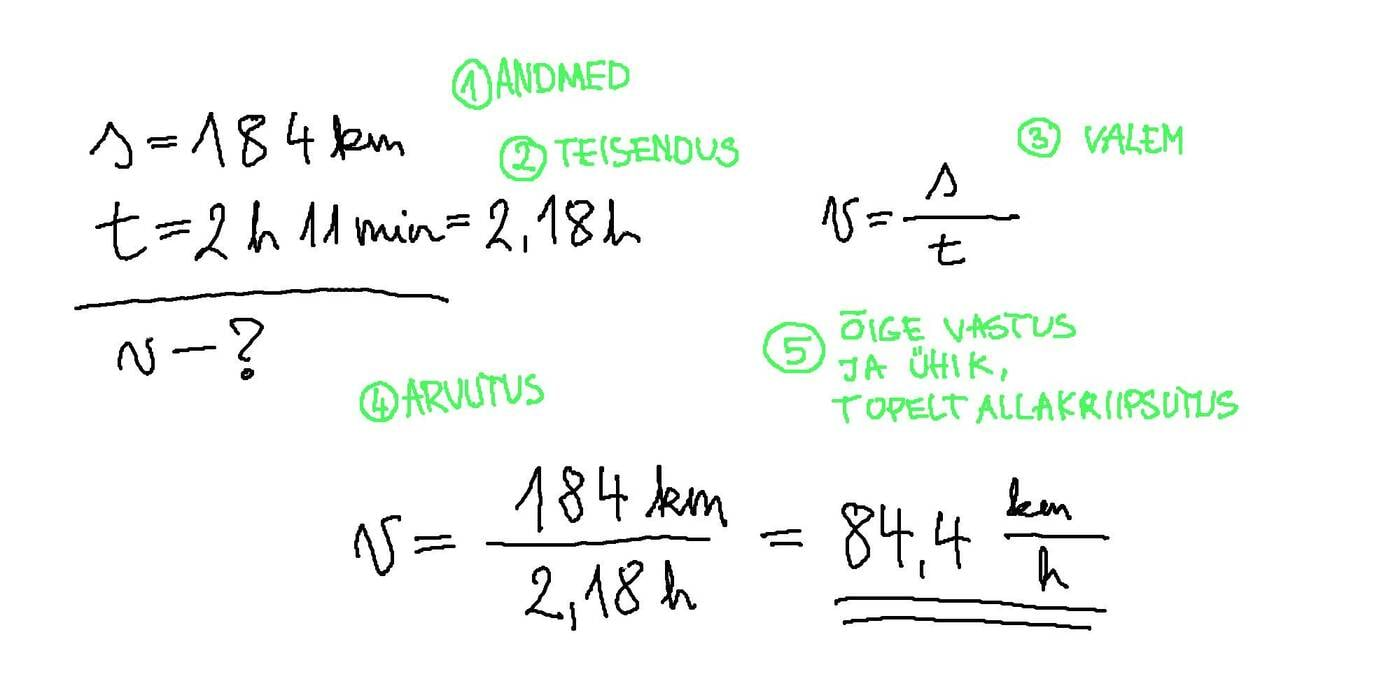
Billy, Bobby ja Bo arvutavad.